数列と説明
下の表は十段までの知恵の輪の操作の節目(カケカエ)をまとめた表で、何段でも規則的に数列を増やせます。
表の左上隅の”一段づつ移動”と書いてある方法は、私が最初に考えた方法で一段目から二段目、二段目から三段目と順番に深い位置に入れていくやり方ですが、手数が多く今は使っていません。
右上隅の”外れた状態⇔N段目”と書いてある方法があることを後で見つけました。この知恵の輪を最少手数で出し入れする方法です。説明もこの方法で書きました。N段に入れる最少手数は、2N+1-(N+2)
の式で求まると考えています。
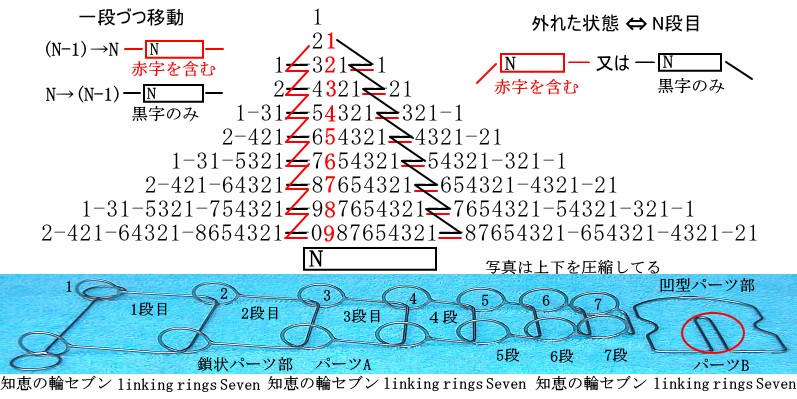
この知恵の輪では、パーツAのどちらか一方の連続した環しか使いません。上の表から三段目への出し入れは、1−31−21と2−321−1の二つの方法で真逆の関係にあります。
1−31−21とはパーツBのU字状に凹んだ部分(上写真赤丸部で以後”B棒”と書く)に1を被せ、クネクネしてB棒に被っている環を外して、31をB棒に被せクネクネして,B棒に被っている環を全部外して、21をB棒に被せクネクネすることです。
”クネクネ”の説明を書くのは難しいのですが、この部分が知恵の輪の実際の操作です。YouTube上の動画の初級編を見れば、操作の流れは分かると思います。”クネクネ”は規則性のある簡単な操作の繰り返しで、一度覚えると忘れません。重要なのは上の数列です。
ハノイの塔や九連環でも見られる様にそれぞれ独特の繰り返し(ここではクネクネと表現している)が”セブン”にもありますが、三段目、四段目と実際に操作を進めていけば自然に身に付きます。
上の表から七段目に出し入れする部分を抜き出すと、1−31−5321−754321−654321−4321−21と2−421−64321−7654321−54321−321−1の二つの方法がありますが、実は互いに真逆の関係にあり、前者の操作の逆が後者です。
入れる時も出す時も同じ操作で、どちらかの数列を選べますが奇数段の時は奇数から始まる前者、偶数段の時は偶数から始まる後者の方法がやり易いかもしれません。
*********************************************************************
下の図で右回り(黒矢印)は1、3、5、7と奇数で始まり、
真逆の左回り(赤矢印)は2、4、6と偶数で始まります。
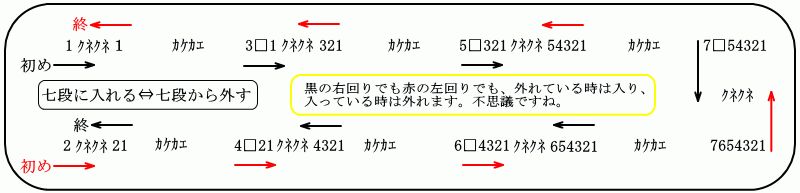
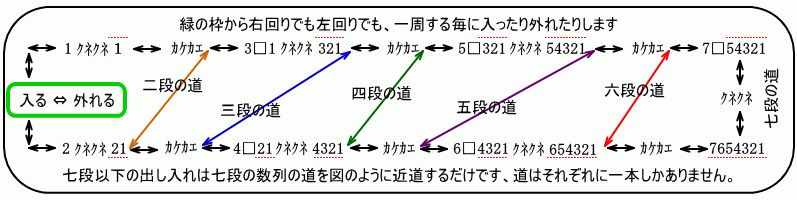
*********************************************************************
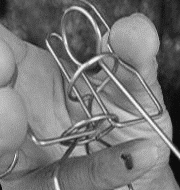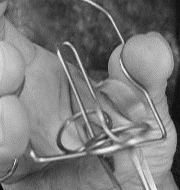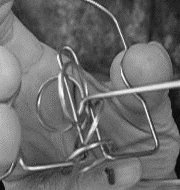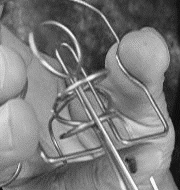
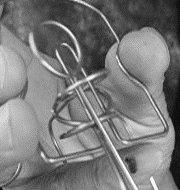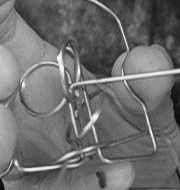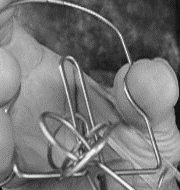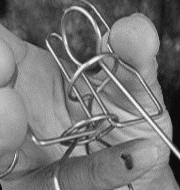
入れる操作の時の(1−31−5321)が前処理的な操作で、次の(754321)をクネクネすると(7654321)となり(左下写真)この時点で七段目に入っていますが、同時に一から六段目のすべてにも入っています。(7654321)をB棒から外し、(654321)をB棒に被せます。ここからが後処理的な操作で(65,43,21)と二段ずつ外れていき、七段目にだけ入った状態になります。
右下の写真は外す操作の時で、(1−31−5321)が前処理的な操作で、次の(754321)をクネクネすると(7654321)となりますがこの時点で七段目が外れて、一から六段目のすべてに入っている様な状態です。入れる時と外す時では操作は同じでも、知恵の輪の状態は当然違います。


左の写真は完全な入れ子状態 右の写真は七段目が入れ子ではない
*********************************************************************
完全な入れ子状態


完全な入れ子(Nesting)状態はすべての段が凹型パーツ部に入っています、このまま戻れば全部外れますが七段目だけB棒から外して架け替えて戻れば七段目だけが凹型パーツ部に取り残されて七段目に入れた事になります。
完全な入れ子状態は次の二段(存在すれば)を完全な入れ子状態に入れる事が出来ます、又逆に二段づつ入れ子状態を外す事ができます、これが”入れ子の法則”です。論理的には何段に増やしても解ける理由です。
下の写真も完全な入れ子になっています。




*********************************************************************
この知恵の輪の手数は定義の仕方で変わりますが、九連環と同様に考えれば、凹型のパーツのU字状にへこんだ隙間を環が通過する回数です。一段目から七段目を実際に数えてみると、1手,4手,11手,26手,57手,120手,247手でした。
それぞれの手数の関連を調べると一段増すと二倍プラスその時の段数という関係にあり、たとえば二段目は1x2+2=4、三段目は4x2+3=11の様になります。これに当てはまる式は、段数をNとすると 2N+1-(N+2) です、また下図左部分の様に各ステップの操作中の段数と同じ桁数の2進数の最大値(全桁1)を合計しても手数と同じになります。
下図は七段に入れる時に奇数から始める数列を使っています、外す時は真逆にします。この方法の時”入れ子”の状態が一番わかり易い様です。赤線部がすべて入れ子でこの段すべてが凹型のパーツに入っています。1,321,54321,7654321と二段づつ入れ子にしていき 654321,4321,21と二段づつ入れ子を外していきます。
下図の点線枠内は入れ子の操作をわかり易く表現する為に、アルファベットに置き換えました。アルファベット四回の間に一手が三回入ります、操作は概念的に”戻して一手、進めて一手、戻して一手、進める”でアルファベット部は二往復で元のままです。間の三手が新しく入れ子になる(又は外れる)二段分の手数(二進数で11)です。入れ子の段(赤線部分)を二進数の1に対応させると、入れ子の操作手数は一致します。
アルファベットの手数はすべて違いますが、全部が連続した入れ子と言う点で性質が”A”と同じと見なす事ができます。見なしたアルファベット部には次の二段を入れ子に出来ます。逆も当然同じです。何段になっても、点線枠内の同じパターンの繰り返しです。Cの中にBが、Bの中にAが又Eの中にDがあり操作も入れ子です。
七段に入れる時に偶数から始める数列(下図では右下の2から左上の1へ)を使うと、6と7の入れ子の位置が入れ替わります(黒線部)がその他はすべて同じです。どちらから初めても入れ子を増やして進み、入れ子を減らして戻ってくるのです。始めに七段目に入っていたら外れ、外れていたら入ります。
N段の”セブン”にはN回の入れ子操作をします。それぞれの手数は操作中の段数をnとした時2のn乗マイナス1です。”セブン”とは、2の3乗マイナス1(七手の基本パターン=B)から名付けました。
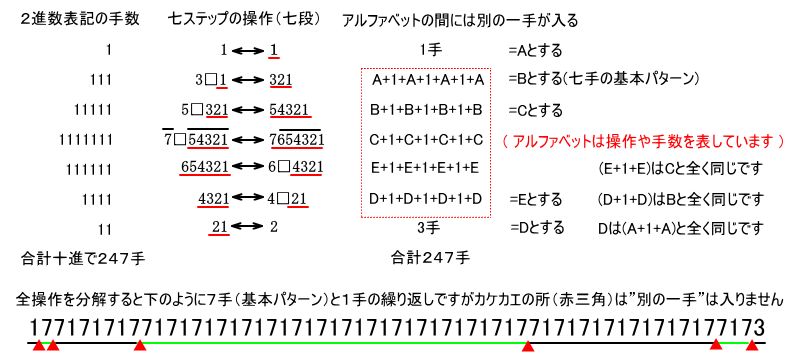
基本パターン(7)は往路と復路を交互に繰り返します、別の一手(1)は常に変化します
31→321(往路) 321→31(復路)
